42 - Other ways to design Low pass Filters for HF use (spreadsheets)

A previous post discussed low pass filters and mentioned six methods of designing them. I covered method 1 and 2(a) in my last post. Here are notes on all six methods...

Method 1:  https://rf-tools.com/lc-filter/ is very very useful, together with the toroid coil turns calculator at http://toroids.info/ this are my main tools until recently when I wanted to investigate more thoroughly. 

Method 2(a). Elsie, ( http://tonnesoftware.com/elsie.html )

Other common design filter software is AADE ( at  http://www.ke5fx.com/aadeflt.htm ) or the PC software at http://www.alkeng.com/ and a number of tools that WEs Hayward included in his EMRFD book, sometimes included in the CDs that come with the ARRL or RSGB handbooks. My personal choices at present are to use the rf-tools website, the elsie software or the spreadsheet in 2(b),or my own written to generate more detailed LTspice circuits to play with.

Method 2(b) A spreadsheet written by Per Magnusson and described in his blog at https://axotron.se/blog/tool-for-designing-butterworth-and-chebyshev-filters/ is available for free download at the same address, he has kindly placed it in the public domain.  The really powerful convenience of the spreadsheet is that clicking a button generates a LTspice schematic (better layout than ELSIE)  I have a sophisticated set of commands for LTspice filter designs and I can quickly get what I need. It uses the table method which I investigated below.

From Per's spreadsheet. clicking the button generates an LTspice schematic

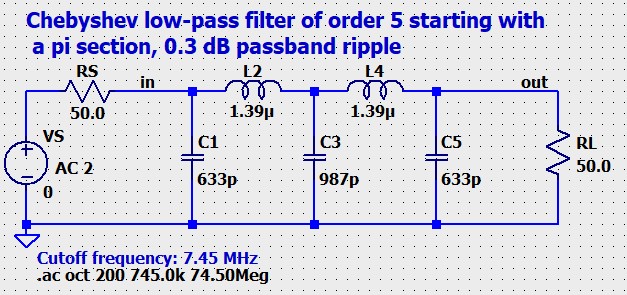Automatically generated from PER's Spreadsheet

You can add all the .Measure commands given in my last post to experiment with this design, add Rser to the coils and capacitors to take the Q factor of real components into account and switch to standard value capacitors or combinations of 2 (or more) capacitors in parallel (typically) to get close to the theoretical values above. It does require Microsoft excel and macros and I tend to use libreoffice, I may convert Pers macros to ones that tun under Libreoffice some day...

Now, I did not realise at first that Pers spreadsheet actually calculated its own tables from scratch and I assumed it was just using lookup tables, so I set about learning how to work out the filters from the raw mathematics. This was a journey that took me some time but was satisfying (in the end!)

The theory behind designing filters allows the use of a calculator. You'll need a scientific calculator, and if it doesn't have cosh functions you'll need a few extra formulae to get around that.

cosh(x) = 1/2(e^x + e^-x)   and Cosh-1(x) = ln(x +/- Sqrt(x^2-1)

I got the theory from a book "Introduction to Radio Frequency Design" by Wes Hayward, W7ZOI, my copy is a 1996 edition and I have misplaced the software that came with the book, but he outlines the equations in Chapter 2, Page 62, I list his equation numbers below page numbers are for my first edition. (Pers also lists references with page numbers in the documentation part of his spreadsheet)

For a 1 Ohm, Butterworth filter components are given by G(k) = 2 SIN(2k-1)* PI/2N where k=1,2..n WEs describes this as equation 2.7-4 on page 61

For the Chebychev, a bit more work is needed. You need to take into account the passband ripple factor E and calculate Chebychev polynomials for the particular order you are designing for.

The ripple factor E=sqrt[10^(R/10)  -  1] where R is the ripple in dB  Eqn 2.7-8/P62

The transfer function H(jw) = SQRT (  1/[1 + E^2 * Cn(w)^2 ]  )       Eqn 2.7-6/p62

Where Cn(w) = cos(n * cos-1(w)) ;w<1 (passband)                             Eqn 2.7-7/P62

Where Cn(w) = cosh(n * cosh-1(w)) ;w>1 (stopband)                         Eqn 2.7-7/P62

To work out component values, Wes replaced the COSH functions with their e equivalents which is handier on most calculators.

d=A/8.68589   Eqn 2.7-11 where A is the passband ripple in dB

B=1/2n * ln [  (e^d + 1)/(e^d-1)]     Eqn 2.7-12    B0=2nB     Eqn 2.7-13  N=1/2(e^B-e^-B) Eqn 2.7-14

ak=sin[  (  (2k-1)Pi)/2n ] ,  bk= N^2  + sin^2(kw/n) ;k=1,2...n  Eqns 2.7-15 and -16 /Page 64

The gk values of the components is then found from g1 = 2a1/N    Eqn 2.7-17/P64

and gk= (4a{k-1}ak)/b{k-1}g{k-1})    Eqn 2.7-18/Page 64 curly braces are for subscripts

I tested these equations in my own spreadsheet -Method 2(c)

Look at the files section of this blog for a link to my google drive for this

Method 3: The GQRP club website has example designs at https://www.gqrp.com/Datasheet_W3NQN.pdf

Here is a screenshot

https://www.gqrp.com/Datasheet_W3NQN.pdf and see QST Feb 1999

Method 4: Using tables that are based on 1 Ohm and 1 Radian/Second frequency (0.159Hz) and scaling them up -to 50 Ohms and as many MHz as you need. - a simple multiplication and division. Note there are some tables about that are scaled to 1MHz or even 1HZ so follow the instructions that come with your tables. There is one Butterworth table (if input and output impedances are the same) but there are separate tables for each degree of ripple in a Chebyshev design so pick the right table. There are also tables that allow for the source, driving impedance to be different to the terminating impedance. I prefer to design a 50 Ohm in and 50 Ohm out filter, add an impedance changing section and merge the various components.

Here are two screenshots of a Butterworth table and the scaling calculations as well as the final values

Again, the file is in my google drive - accessible from the pages section of this blog

In practice I just use the RF-Tools website, Elsie and Per's or my own spreadsheets!

To conclude, here are a list of references and bibliography I found and read!

[1] EMRFD, Experimental Methods in Radio Frequency Design, by Wes Hayward (Author), Rick Campbell (Author), Bob Larkin (Author) I have the first edition, there is a second. This was the most valuable resource, everyone should have a copy of this book!

[2] RF Design Basics by  John Fielding, ZS5JF has a good chapter on Filters.

[3] ARRL Handbook, older editions are more detailed

[4] RSGB Handbook, The older editions are better as they cover the table method, modern versions just say " use online or downloadable tools"

[5] Zveverev's "Handbook of Filter Synthesis" I was able to download a copy from https://ia803101.us.archive.org/20/items/HandbookOfFilterSynthesis/Handbook%20of%20Filter%20Synthesis.pdf so I assume it is out of copyright. It is a Wiley book, dated 1967. This book contains all the tables that more modern books quote. It is a heavy read but a good reference.

[6] Part 1 and Part 2 of Design of Microwave filters, impedance matching networks and coupling structures Volume 1 and 2 by G.L. Matthaei, Leo Young and E.M.T. Jones, available from download from https://www.microwaves101.com/uploads/MYJ-part-1.pdf

[7] G3OTK, Richard Harris's 9 part series of articles at Itchen Valley Amateur Radio club  https://www.ivarc.org.uk/uploads/1/2/3/8/12380834/1_filter_article_version_2.pdf

41 - Design and Analysis of Low Pass Filters (Copy of part 2 of an Article for CONTACT )

Designing and Analysing Low Pass Filters for RF (HF) use Part 2: MI5AFL

Method 1: https://rf-tools.com/lc-filter/ is very very useful, together with the toroid coil turns calculator at http://toroids.info/ or coil64.exe from http://coil32.net ) for air-cored coils, these are my main tools until recently when I wanted to investigate more thoroughly.

Here is an example screenshot: There is a simple graphical plot of performance and cursors that allow moving around the graphs - I prefer to copy the circuit over to LTspice to investigate whether 5% or 2% capacitors are needed, to try standard values and to play with the Q of the coils, etc.,

Above is a screenshot of the RF-Tools.com design tool, it plots the amplitude response - the plot of attenuation with frequency is called S21. It also plots, in red, the return loss or S11 figures in dB - this is related to the VSWR or how well the filter matches to 50 Ohms. I usually redraw the circuit in Ltspice and simulate in detail there - moving the cursor about on the RF-tool is tedious and I am well practiced in how to use LTspice effectively. I will cover the LTspice simulation after discussing Elsie.

Method 2: Elsie, (from http://tonnesoftware.com )it took me a while to get familiar with this software but once I had the hang of it, I found it useful. I was particularly interested in designing a filter for the 40m band that had around 35dB of second harmonic rejection (which since I was using a push-pull amplifier I expected a further 15 to 20 dB from the balanced nature of that circuit) and I also wanted at least 50dB rejection at 21MHz - the third harmonic. I also wanted good SWR (Return loss) at the input, assuming 50 Ohm.

To use ELSIE you click on a couple of screens; first hit the DESIGN button and fill in a form, note the software describes the corner frequency Fc as the ripple bandwidth - technically correct since a LPF starts at zero and goes to the corner frequency for its passband, hence the ripple bandwidth is the “passband”. After hitting the design button click the ANALYSIS button to set the parameters for the plot - the start and end frequency. You can set the Q of the coils and capacitors and the reference impedance for VSWR method - I set this to 50 Ohms.

Now click on the SCHEMATIC button to see the circuit diagram, complete with calculated values. I usually click on the “show Q-Value resistances as I may use these values in LTspice later.

Click on the PLOT button to get a useful plot. click the second icon down on the left hand side to get both S21 and S11. I also set 7 Markers and clicked the markers menu item to show them, they are very useful.

This is bit hard to see so here is a zoom in to the Marker results at the foot of the diagram above.

The yellow boxes show interesting stuff. We optimise these by moving Fc up and down a bit, if we can’t meet our specifications we go back and change the order from 5 to 7. The markers below are for a 7.45MHz Fc and 0.1dB ripple, 5^th order. It is the result of my experimenting with Elsis and has the lowest insertion loss with a reasonable harmonic rejection. I used a design Q of 200 for the coils and 2000 for the Capacitors. Later I changed the Q to 290 and 10,000

Since good (big) return loss coincides with lowest insertion loss you can see how optimisation works by imagining the 1 to 5 markers on the red graph sliding downwards into the trough.

The nice thing about ELSIE is that if you nip back and make a change to the design data, the plot and the markers change immediately, you can go back and forward experimenting very quickly to get what you need. Here, I see the VSWR is below 1.09 and the insertion loss is less than 0.16dB which is about 1.7%. (see http://www.sengpielaudio.com/calculator-db.htm ) The harmonics are 32dB and 51 dB down so all is good enough. I also tried 7.2MHZ and 7.25MHZ but 7.45 is the best compromise. LTspice gets better figures after I design the air cored coils (15mm former and 1.2mm wire at 2.4mm spacing gives a Q or 290 according to Coil64.exe)

Finally if you click the WRITE button you get the option to write an LTspice .ASC file which is what LTspice uses. You can save it and then launch LTspice and load it as is, but I prefer to add some extra commands to the LTspice schematic as you'll see below. I usually run three different simulations, the first confirms the results above, I then “design” the inductors using Coil64.exe and this gives a computed Q and RESR value, I modify the capacitors to standard values and edit the LTspice schematic and re-simulate to check the performance. Finally I use the Gaussian and, lately, Worst case simulations to vary the component tolerances see how careful I need to make the filter. (see the October 2020 issue of the CONTACT magazine for details of using the Gaussian formulas)

To use Ltspice effectively you need to know how to use .MEASURE text commands. Also there is a choice as to how to display S21 and S11. There is a .NET command but Wes showed a “trick” on his website ( https://w7zoi.net/Extract-sp.pdf ) of how to add S11 and S21 labels directly to the schematic – this just makes plotting a bit quicker so it what I use.

It uses a voltage source with an internal resistance of 50 Ohms and a driving voltage of 2 volts, this gets divided to 1 volt at the actual input to the filter and so the output voltage gives us S21 directly ( the gain is Vout/Vin and Vin is ‘1’). Likewise subtracting one volt from the actual input means that what is left is what gets reflected back from the filter. So the second voltage source gives us the reflected voltage, again this scales by ‘1’ to give us S11 directly. We add a one GigaOHM resistor in series with this subtracting voltage to avoid distorting the results.

We can use LTspice for simple plots, and then alter the capacitances to preferred values.

A more advanced use of LTspice is to show how the performance varies as components vary. You can do multiple simulations with each value set at its worst case or you can vary a value thousands of times between its worst case values, a 2% capacitor can be between 98% and 102% of its nominal value. Here is the spread of performance values after 2000 simulations.

You can't know which component variations causes which value but it looks like it should be alright, you can estimate by eye the chances of your physical circuit meeting the specification. It should convince you that you should never make a filter without (a) checking the values of the components before soldering them in and (b) to check the performance of the completed filter. Thank goodness for the NanoVNA, £50 well spent – get one!

I have found a new, better way to perform an analysis. It is much quicker to pick the worst case extremities of each component and just analyse this, for 5 components there are 32 possible combinations of each component being too high, or being too low (at the limit of its tolerance, +/-2% or +/-5% ). An application note by Analog Devices shows a technique using two one-line functions to iterate through all 32 cases. It uses a 5 bit binary number and we can work backwards to see what component combinations give a particular result. This is important as it opens the opportunity to “tune” a filter to be better than its calculated performance.

The diagram below gives the LTspice schematic the result of plotting the values calculated by the .MEASURE statements against the run number. We can convert the run number into a 5 bit binary number and work out what component values cause what results.

Run numbers 8,9 and 10 have very good insertion losses (and return loss – inevitably since RL and insertion loss are related) 8 is 01000 in binary so keeping C1, C3,L4 and C5 at the lower extremeity (98% of nominal) and L2 5% higher than nominal will give the best results.

To conclude, here are a list of references,

https://rf-tools.com/lc-filter

https://toroids.info will work out how many coils on a powdered iron core toroid

https://coil32.net Can calculate turns and the Q of an air-cored coil.

http://tonnesoftware.com/elsie.html Download ELSIE from here (look at the other programs too!)

http://www.sengpielaudio.com/calculator-db.htm A simple tool to convert dB to a ratio

https://w7zoi.net/Extract-sp.pdf How to modify an LTspice schematic to show S21 and S11

https://www.everythingrf.com/rf-calculators/return-loss-to-vswr-calculator What it says!

https://www.analog.com/en/design-center/design-tools-and-calculators/ltspice-simulator.html

You can download the LTspice simulator from the link above, its handy for just drawing schematics too!

Another common filter design software program is AADE ( http://www.ke5fx.com/aadeflt.htm ) or the PC software at http://www.alkeng.com/ and there are a number of tools included in the CDs that come with Wes Hayward’s EMRFD book, and the older ARRL or RSGB handbooks.

My personal choices at present are to use the rf-tools website, the ELSIE software or the spreadsheets I have developed and found hese are also reproduced on my blog at https://MI5AFL.blogspot.com and in my google drive (links are in my blog).