Designing Crystal Filters
Filters are usually used to block out a band of frequencies, you can have low
pass, high pass and bandpass that do what their name suggests. You can also
design notch filters (band-stop) and all-pass filters. All pass filters are needed
because although we tend to fixate on the strength (amplitude) of signals of
different frequencies passing through our circuits; the output voltage versus
the input voltage, we should also consider the time delay of each frequency
as it passes through each part of our system. Such delays are inevitable in the
real world, expressed either as a phase delay or a time delay, we use the term
group delay to plot actual time delays against frequency. Non-linear group
delays can make audio signals sound strange, a harshness that is hard to
describe. This is a topic that deserves more attention in the RF (and audio)
world, it, and ringing, affect digital signals considerably, even RTTY and CW. It
will become more important and modern receivers may well have much
better audio than receivers of old. All pass filters add a different delay to
different frequencies without significantly weakening them. A future article
might look at how DSP can use all pass methods to improve and remove such
distortion. An advanced topic.
In the short term I want to make a complete SSB transceiver based on the
μBITX (https://www.hfsignals.com/ and https://groups.io/g/BITX20/topics ). I
enjoy homebrewing and will build it from scratch. Most radios have only four
types of circuit within them, amplifiers, mixers, filters and oscillators.
Oscillators are very conveniently available as Si5351A or Si570 modules driven
by an Arduino or ARM, the rest is straightforward provided a modular
approach is taken.
In this article I will concentrate on crystal band pass filters and end up using a
simple method with as simple tools as possible. I discussed last month how to
measure the parameters of a bunch of crystals and how a nanoVNA and
spreadsheet are good enough. In truth this is still work in progress, I still have
some concerns over potential inaccuracy in determining Rm and Co. There
are four or five ways of measuring these and I will continue to experiment
and although using a VNA is really convenient and “good enough” it may be
better to augment this with a capacitance meter or simple resistive test jig
(more in a future article or blog entry).
To recap, a crystal can be represented as three components in series: Rm, Cm
and Lm and a fourth component in parallel with these three; Co (other texts
sometimes call this Cp and the motional components are sometimes called
Rs, Cs and Ls). From these can be calculated the Q of the crystal. Better
described as the unloaded Q.
In the old days we used a filter circuit called a Lattice type, it required crystals
to each have different frequencies, which was a real nuisance, expensive or
difficult to arrange. The more common modern filters are of a type called a
ladder filter and this is what I will discuss here. These are designed assuming
equal (or nearly equal) crystal frequencies. The process of designing filters
invariably assumes equal values for the four parameters of every crystal and
is most conveniently done with design software. Sometimes only two or three
parameters are used and then extra capacitance added to ‘tune’ the filter.
Some types of filters don’t need this and I favour simplicity over performance
– if you are only building one transceiver you can afford the luxury of
revisiting the design and fiddling with it once it is working; the beauty of
homebrew! So here is the ‘Mark 1’ filter.
Instead of design software you can use tables of coefficients to multiply and
scale components to suit any desired frequency, bandwidth and terminating
impedances, it can be hard work though and modern software packages
make crystal filter design very easy.
Although you don’t need all the parameters, you do need to preselect your
crystals to be as close as possible to each other in frequency, ideally within
2% of the bandwidth of your chosen filter – to design an SSB 2.2 kHz filter
requires crystals to be within 44 Hz. To design a 350 Hz filter for CW requires
(ideally) crystals to be within 7 Hz! older texts stated getting within 5 to 10%
‘will do’ often producing in-band ripple which is not necessarily noticed when
reading CW at a single frequency.
There are a number of software packages available free; such as the AADE
software (http://www.ke5fx.com/aadeflt.htm ) which is now free but didn’t
used to be. The Elsie design package is paid for but has a free limited version
(http://tonnesoftware.com/ ). If you have bought the book by Wes Hayward
‘Experimental Methods in RF Design’ then it comes with a software suite that
includes LADPAC and XLAD as well as XTUNE and others. Every homebrewer
should own a copy of “EMRFD”. The ARRL handbook (another invaluable buy)
often comes with a CD with design software but here I will use a software
program known as Dishal but you should experiment with the others to see
which suits you.
I will be using Dishal version 2.0.5.2, You can get it from
http://WARC.org.uk under the technical tag or google to find it.
To experiment does not mean spending money buying crystals and hours
soldering up circuits; use simulation. The LTSpice simulation software from
Analog Devices (https://www.analog.com/en/design-center/design-tools-
and-calculators/ltspice-simulator.html ) allows drawing a circuit (schematic in
US English) comprised of crystals and capacitors (and other things as needed).
Note that the XTAL symbol in in the ‘Misc’ library folder and you set the
crystal parameters by right-clicking on the symbol, the first parameter is Cm
and the series inductance and resistance are Lm and Rm whereas the parallel
capacitance is Co.
You must apply a voltage source of known internal impedance that can sweep a range of frequencies – e.g. 5 kHz either side of the filter’s bandwidth and delivering the output into a load impedance where the output voltage (and phase) can be captured and plotted against frequency. You must adhere to a filter’s designed input and output impedance if you are to get the correct, designed, response.
Applying filters in the real world will inevitably require matching circuits at the input and output as it is too difficult to design filters with standard 50Ω inputs and outputs. A simple ferrite toroid transformer at the input and a capacitor to
ground may do or a matching network can be designed by using an online
calculator that can also design the toroids e.g. at http://toroids.info.
A few notes about Filter types: not all software covers all types, I list a lot of
them here but it is convenient to use QER types in homebrew as they are
simplest, they are a recent development – I can find no reference to them
prior to 2010 and older textbooks do not cover them. Commercial filters are
often 0.1 dB ripple Chebyshev types, as least for SSB, FM and AM use. They
do not do well passing narrow band digital signals where Bessel types are
best at reducing bit errors.
The criteria to use when choosing a filter type include; convenience and
cheapness (of course!) but also the desired bandwidth, the insertion loss, the
steepness of the side slopes, the amount of in-band ripple, the input and
output termination impedances and how these change with frequency (i.e.
the return loss (SWR) across the full frequency spectrum). The group delay i.e.
the linearity of the time delay versus frequency is often ignored but affects
ringing and how well audio sounds as well as how many bit errors digital data
will create.
Butterworth type: This has a smooth response in the passband with no
ripples but the side slopes not as sharp as some other types. They need
capacitors of varying values (in pairs as the schematic is symmetrical), ideally
you need to add some series capacitors to the centre crystals or pick crystals
at very slightly different frequencies to the ones at the beginning and ends of
the filter. This is true of the Chebyshev types too. Butterworth have lower
insertion loss than Chebyshev types.
Chebyshev type 1: have sharp slopes but have ripple in the passband, you
have to choose how many dB the ripples should be when you do your design.
You won’t notice 0.1dB. Insertion loss increases with order (the number of
crystals) and with higher ripple. Technically there are two types of Chebyshev
but we normally use type 1 (type 2s have ripples in the stop band)
Elliptical type also known as a Cauer: have ripples in the passband as well as
very large ripples in the stopband – you can often use this to advantage if
designing LC low pass filters – the first trough in the stopband can be made to
coincide with the second harmonic of the pass frequency giving really good
harmonic suppression. This is not that relevant to narrow passband filters.
Bessel type: Good constant group delay characteristics, average filter slope
and passband ripple with lowest insertion losses, good for CW or data. Linear
Phase types are similar, with slightly higher insertion loss but a better shape
factor (steeper sides). The Gaussian types: have better shape factors than
either the Bessel or linear phase but slightly worse group delay. You typically
choose what is called Gaussian to 12 dB or Gaussian to 6 dB or just a
Gaussian type. These are all good for CW or data. They are hard to interface
to as their return loss varies a lot.
Cohn Min-Loss type : These have in band ripple but all the capacitors have
the same value, the QER is better. The ripple in the passband increases a lot
with increasing order and below 500 Hz width 6 order they ring a lot
QER type have the major advantage that all its capacitors have the same
value like the Cohn but there is less ripple in the passband. This is at the
expense of needing an extra couple of crystals that do not increase the order
of the filter. Its insertion loss is less than the Cohn too. Good for SSB.
I will concentrate on the QER type as it is the simplest and has reasonable
performance. It is even possible to make QER filters with no mathematics and
no software, just by experimenting. It is very difficult to make the other types
this way as they have too many interrelated components. The blog of W3JDR
describes how in his July 2017 entry
(https://w3jdr.wordpress.com/2017/07/31/qer-crystal-filter-designer) but it
is easier to use the Dishal software or the table/equation method.
This schematic above shows an 8th order filter, you don’t count X1 or X10
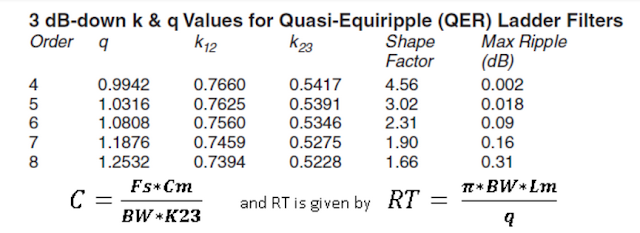
The table below lists q and k coefficients and applying these to the equations
for C and Rt is straightforward to calculate, they ignore the parallel
capacitance Co of the crystal and the series resistance Rm but they are a good
starting point.
Alternatively, it is much easier to use the DISHAL Software as it has an option
to design QER components that appears to correct for Cp (commonly called
Co) the screenshot below shows the form you fill in after running DISHAL, the
screenshot is from version 2.0.5.2 click on the QER menu item on the top line
after running DISHAL.
As you see, you supply Lm and Cp, tell it what frequency your crystals are and
what bandwidth and order you want. It tells you to use 49.3pF capacitors and
that the input and output impedances are 252.8 Ohms. The frequency will be
slightly off too. The next stage is either to build it or to simulate it. We can
then change the components to 50pF and 250 Ohm Zin/Zou and see what the
filter response looks like. An advanced topic is to simulate the filter with
actual parameter values for each crystal and not just assume that all crystals
are absolutely identical. You can move your crystals around and pick the best
arrangement before building. This is a new idea I have not seen before. This
still needs further work as I think the NanoVNA is not reporting the Rm value
accurately enough although its frequencies are stable.
My QER Filter
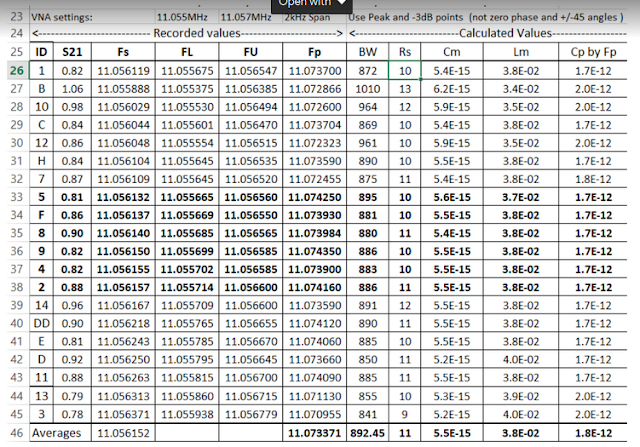
I have a batch of 20 crystals and want to make a 6 pole QER filter. I have
measured these using my NanoVNA as described in last month’s article. Here
is the relevant section from the spreadsheet stored on my blog
http://mi5afl.blogspot.com/p/blog-page_15.html. The file is called
‘Calculating_XTAL_Parameters_with_a_VNA.xlsx’.
I also measured Co by a capacitance meter and got values around 3.3 pF, not
sure which is the correct value – measuring small values of picofarads is
difficult! Also, I should have recorded S21 more carefully, three significant
figures and I need to recheck the figures - I have actually ordered a new
nanoVNA (a V2 to allow antenna analysis at 2.4 GHz to allow me to make WiFi
helixes!) and am making up the G3UUR crystal jig to allow comparisons.
I picked the values in bold as they are all within 15 Hz of each other, then
created a schematic in LTSpice, initially using the average values to confirm
the Dishal design.
Note to use LTspice for verifying crystal filters you need to use the XTAL
symbol found in the ‘misc’ library when you select the ‘insert component’
option. Also, you do not enter a frequency value for the xtals – you enter the
series inductance and capacitance values Lm and Cm and the resonant
frequency is calculated for you. In fact you should enter values for Rm (known
as Rser) and Cp (LTSpice calls this Cpar and some texts use Co).
Place the XTAL symbol on the
schematic and right click on it
and you should see the left-hand
window; Note the units of
‘femtofarads’ for Cm.
You may also want to have these values visible on the schematic.
To do this hold down the control key and click on the XTAL symbol,
the window below for the “Component Attribute Editor” should appear.
Move the cursor to the Vis. Attribute and right click to place an ‘X’ in the appropriate cell.
Once you have the schematic as shown you can run the simulation, click on
‘out’ to get the filter response. You may need to do some maths to get an exact filter loss in dB so watch out that you read off the correct input and output voltages. Note the bandwidth below is actually 1.76 kHz bandwidth and the shape factor near 2, which is a good narrow SSB filter that suits my ears, some people prefer 2.2 kHz widths...
When I add LC matching and put in actual measured parameters for each
crystal and standard component values for the capacitors, I have the
schematic below;
And this gives a response with similar bandwidths – 1.85 kHz.
In summary, you can use the DISHAL software to quickly design filters, you
can use LTspice to verify the filter response and you can alter the LTspice
schematic components to experiment without having to build many versions
of a filter.
References and bibliography:
The ARRL Handbook 2015. The two pages of section 11.6.2 ‘Crystal filter
Design’ (and all of chapter 11!)
Experimental Methods in Rf Design by Wes Hayward W7KOI, Rick Campbell,
KK7B and Bob Larkin, W7PUA. The 8 pages of section 3.4 ‘Crystal Filters’ Page
3.17 onwards
Horst Steder, DJ6EV and Jack A. Hardcastle, G3JIR, ‘Crystal Ladder Filters for
All’, QEX Nov/Dec 2009, P14-
Dave Gordan-Smith, G3UUR ‘Further Thoughts on Crystal Ladder Filter
Design’, The QRP Quarterly, Spring 2010.
Randy Evans, KJ6PO, ‘Crystal Parameter Measurement and Ladder Crystal-
Filter Design’, QEX, Sept/Oct 2003, P38-
J. A. Hardcastle, G3JIR, ‘Ladder Crystal Filter Design’, QST November 1980
Wes Hayward, W7ZOI, ‘A Unified Approach to the Design of Crystal Ladder
Filters’, QST May 1982, P21-
Wes Hayward, W7ZOI, ‘Designing and Building Simple Crystal Filters’, QST July
1987, P24-
Bill Carver, K6OLG, ‘High Performance Crystal Filter Design’, Communications
Quarterly Jan 1993, P11-
Wes Hayward, W7ZOI, ‘Refinements in Crystal Ladder Filter Design’, QEX,
June, 1995. P16-