An Amplifier amplifies! a small signal going into the input produces a bigger signal at the output. What are the relevant details? The parameters that matter.
Gain: a gain can be expressed in several ways and you must be clear if it is Voltage gain or Power gain. If the input impedance and output impedances are the same then these are simply related. If not you have to convert from one to the other at the input and also the output and manually work out each gain separately, simple enough using Ohm's law
Gain can be expressed as a number such as 10, again, you need to know if this is a voltage gain or power gain. If one amplifier is followed by another then you multiply the gains - if expressed as numbers. If the second amplifier has a gain of 8 then the combined gain is 80. It is also common to express gain in decibels, these are calculated by taking the logarithm of a gain number (and multiplying by 10 if it is a power gain or by 20 if it is a voltage gain. When you have two amplifiers connected together and you know their gains in dB you add these to combine them - if one has a gain of 10dB and the other has 9dB then the combined gain is 19dB. Addition is easier than multiplication which is why dBs are popular.
Bandwidth: The upper and lower frequencies where the gain drops by 3dB, in power terms this is a drop of 50%, in voltage terms it is a drop of 29.9%.
The parameters above are easily tested; a signal generator and oscilloscope will show the voltage response, particularly if you use the oscilloscope to look at the input voltage at the same time as the output voltage. Voltage Gain is Vout/Vin. You can use peak voltage, peak to peak voltage or RMS, as long as the waveforms are the same shape, preferably sinewaves and you are consistent between measuring input and output and there is no distortion. If you express Vout/Vin as a number, e.g 7 you can convert this to dB by taking the base ten logarithm of 7 and multiplying by twenty which gives about 17dB as Av. It is important that the amplifier sees a load at the output, usually 50 Ohms. It should also be driven by a source with the same internal impedance that the amplifier will see when it is used in a final system, again often 50 Ohms. Your signal generator might have two outputs, with a Internal Impedance of 600 Ohm or 50 Ohm. Pick the right one or add an external attenuator.
You don't even need an oscilloscope although you can't just use your DVM or a voltmeter directly since they don't work at frequencies above audio (and maybe not even at audio) but you can use a simple diode detector with your DVM. These can even read power directly - see the RSGB handbook. You could even make a simple signal generator if you are testing on a budget.
if you know Zin and Zout of the amplifier you can work out the power in and power out (Square the voltage and divide by the impedance) and this gives you the power gain. You can express Power Out divided by Power In as a simple number or in dB, e.g if the ratio is 49:1 this is a power gain of 17dB. To convert to dB you take the base ten log and multiply by ten. We usually use power in RF work.
With experience you probably will memorise a few conversions to make your life easier. 3dB is 2:1, 6dB is 4:1, 9dB is 8:1 - do you see the pattern here? adding 3 to the dBs doubles the ratio. Likewise 10dB is 10:1, 20dB is 100:1, 30dB is 1000:1. The pattern here is that the digit in front of the zero of the dB figure tells you how many zeros to put in the ratio after the leading '1'. This is only true for power ratio and the equation 10Log(ratio) As an example, note that 36dB is 30dB + 6dB and this is a ratio of 1000 to 1, multiplied by a ratio of 4 to one so it represents 4000 to 1.
If everything is 50 Ohms you can usually read of the mW or dBm scale of your signal generator. You will need to add a dummy load to the output if you are using a normal oscilloscope. Alternatively you can use a Spectrum Analyser(SA) at the output. These usually have an internal impedance of 50 Ohms by design. The SA has the advantage that its display is in dBm directly. Provided your output is meant to be driving 50 Ohms. You must attenuate the output if it might overload the Analyser. I use a £100 SDRPLay RSP1a and a homebuilt attenuator.
dBm's are the ratio with respect to 1mW so 36dBm would be 4000mW (i.e 4 Watts). dB's are just a numeric ratio, dBm are an actual, absolute power. You will also sometimes see dBV or dBuV. There are actual voltages, not just ratios. I discovered lately that FFTs in LTSpice are displayed in (rms) dBV and you need to add 13dB to get dBms. That is not in the manual!
There are lots of calculators online to convert dB to ratios, dBv, dBuv or dBm or dBWs. You often must know the relevant impedances for these calculators to work, they usually assume 50 Ohms. E.g https://www.rfmentor.com/content/dbm-dbw-dbuv-calculators
It is most convenient if the SA has a tracking generator and then you can get a direct plot of the frequency response. If not you have to pick different frequencies and plot graphs in graph paper or in a spreadsheet (Excel can "join up the dots" for you). If Zin and Zout are 50 Ohms you can use a NanoVNA, and the NanoVNA can even measure/check Zin and Zout. But you frequently need attenuators at both the output of channel 0 (port 1) and channel 1(port 2) of your NanoVNA, the first protects the amplifier (DUT - Device Under Test) and the second the input of the VNA - it needs to be below a milliwatt.
I repeat do not apply the NanoVNA to a circuit unless it can cope with a milliWatt (0dBm or 1mW) Do not apply the output of a circuit to the NanoVNA input unless the circuit is outputting less than a milliwatt. If using a Spectrum analyser or SDR acting as a spectrum analyser this also applies.
If Zin and Zout are not 50 Ohms you can still use 50 Ohm based instrumentation as they will indicate performance if you are going to use the module under test in a 50 Ohm environment - fed by an antenna or other module output with 50 Ohm internal impedance and feeding into the next stage where its input impedance is 50 Ohms. This is how a normal RF system works, 50 Ohm feeds 50 Ohm, if both are the same you get maximum power transferred from one stage to another. And keeping at 50 Ohms keeps the effects of stray capacitance low. If you insert an attenuator (designed for 50 Ohm systems) between stages you restore the effective Zin or Zout back to near 50.
No discussion of Zin and Zout would be complete without talking about alternatives ways of describing input and output impedances - in the RF world we use SWR or return loss (or reflection coefficient) but I will postpone this for now.
Maximum Input amplitude: (Voltage or current) if you double the input amplitude, we expect the output to double as well. Graphically if we plot input against output we expect a straight line at a certain slope (the gain). The straight line cannot go on forever. A real amplifier has a power supply. Normally the output voltage cannot exceed the power supply.
It can exceed the output voltage or current of the power supply if a transformer is used or if an inductor or capacitor stores energy and then gives it back to the output such that its voltage or current adds to the power supply. For instance a single ended transistor with an inductor as its collector load can output nearly twice the power supply voltage. Nonetheless the output should be the input magnified by a fixed number (the gain). Once the output droops you are nearing the limit.
Linearity: related to the maximum input amplitude. There are several ways of specifying this. In the RF world we use two different methods. If we are looking at the graph of a real amplifier and note that the "straight line" droops by 1dB we call this the P(-1dB) point, sometimes the minus sign is omitted (P1dB) it is an example of gain compression. You could meet an amplifier where the output rises by 1dB but it is uncommon (I've never seen one) You probably should not be running an amplifier beyond the P(-1dB) point and if you are at or near it you are generating a small amount of distortion. If outputting speech you are only distorting on the peaks of speech that take you to the P1dB point, the vast majority of the time you are passing a lower, more linear, signal. This does not apply if you are passing Data or using FM - you might be running at peak output all the time, a good reason to reduce amplitude if using data, apart from the distortion you are stressing the amplifier and its heat sink or its omission is, by design, not able to cope with continuous peak outputs. Be careful overusing speech compression as well.
The other performance metric for linearity/Strong signal handling ability is related to Inter-Modulation Distortion(IMD) and specifically the amount of third order Intermodulation Distortion. There is a strange relationship between IMD3 and Power out (Pout). As you increase Pout(by increasing Pin of course) the IMD3 increases three times faster (in reasonable, well behaved amplifiers)
You can graphically plot a straight line for Pout/Pin and IMD3. since the "slope" of the IMD3 line is steeper it will cross the Pout line at some artificially high Pout - remember at some point well before the crossover the Pout line will droop by 1dB and then droop even further until saturating with a straight line - the power supply cannot supply any more power (your devices may well be glowing red hot by this stage and blow up shortly afterwards or before).
The crossover point is never reached, you have to extend the lines by hand on the graphpaper. It is a theoretical point. The power level where the crossover is drawn is called the third order Intercept point and we use the term OIP3 to represent it. (The Output Intercept Point for third order intermodulation distortion).
You can also mathematically move the figure to the input where it is called the IIP3. You simple subtract the gain (since the figures are in logarithmic dB you subtract rather than dividing by the gain). The IIP3 and OIP3 are important even if they are theoretical. It is easy to work out a combined figure when you have a chain of amplifiers and you can calculate when a strong signal will cause distortion. If you are dealing with a single stage the P(1db) is easier to measure.
There is even a rough rule of thumb that the OIP3 is usually about 10 to 12 dB higher than the one dB gain compression point P(-1db), at least if using ordinary bipolar transistors, FETs are usually show about a 7 or 8dB difference. Crude but useful...
Apart from using the rule of thumb you can use a formula based on a graphical technique. If Pout increases at a rate 'x' and IMD3 increases at '3x' then IMD is catching up with Pout at '2x' if you have a specific measurement of both - usually taken from a spectrum analyser then you can calculate the crossover point, the third order intercept.
For example if the Pout is at 20dBm and the IMD3 is 6dBm then if we "theoretically" increased Pout to 24dBm we would expect IMD3 to go to 18dBm - because it increases three times faster (up 4 and up 12 dBm). If we increase Pout another 3dBm then IMD3 goes up 9dBm so when Pout=27dBm IMD3 would be also 27dBm - the crossover point. An easier calculation is to take half the difference between the real Pout and the IMD3 taken at a specific Pin, the difference in the example above 20dBm - 6dBm which is 14dB, half is 7 and we add the 7 to Pout to get 27dBm. This works because the difference between Pout and IMD3 increases is a factor or 2.
OIP3 = Pout + 1/2 (Pout-IMD3 )
We can do this easily using a two tone oscillator and a spectrum analyser.
Other parameters of amplifiers we would like to measure are;
Input and Output Impedances: Easily done with a nanoVNA (it is what it is designed to do) but we must take into account the strength of the VNA output and add an attenuator for amplifiers used for small signals and we might even want to add an amplifier(of known gain and return losses) to test medium and higher power amplifiers under more realistic conditions. Secondly the output of the device under test may be too strong for the input port of the VNA. Luckily attenuators can be knocked up by soldering three cheap resistors in a "pi" or "T" arrangement.
see https://www.rfcafe.com/references/electrical/attenuators.htm
There is an alternative to a NanoVNA that is cheaper; A return loss bridge (RLB) is a simple device, at its heart it is a simple 4 resistor bridge, with one of the resistors omitted - you put the amplifier input or output in its place. Applying a signal from a signal generator will give no reading at the detector output if everything is 50 Ohms and a maximum reading when either shorted or left open circuited. You can infer the impedance of the amplifier depending on how far away from maximum the detector sees. The detector output needs a Balun or choke to allow it to measure things with respect to ground. You can buy a cheap RLB from Ebay for a tenner, or make one for under a quid. (see https://www.qsl.net/kl7jef/Build a Return Loss Bridge.pdf ) The NanoVNA uses this method and has RLBs inside it - but the signal levels and sensitivity are fixed which is a nuisance sometimes. I will do a future article on RLBs.
When measuring Zout you need to terminate the amplifier input with a 50 Ohm resistor, you should check with a dummy load and scope that the amplifier is not outputting anything, if it is you will damage your test gear. I was nervous measuring Zout - you apply outputs from your test gear to the output of the amplifier, it is wise to check the output is zero before connecting up your nanoVNA, RLB or signal generator! With the input shorted to ground through a 50 Ohm resistor, the output should be zero but it is wise to check, a spurious oscillation might be happening (usually called instability - a bad thing!) Also make sure there is a DC block in the amplifier (there usually is). This can be a capacitor or transformer. Don't apply DC to your nanoVNA or Spectrum Analyser.
Measuring Zout in a non-linear amplifier is of limited use, it varies all over the place. You can pick a particular power out and try and measure Zout at this point. If you cannot use the methods described above, a SWR bridge can be of some use. Alternatively apply a load near what you think Zout is, take readings of both voltage and current (record phase). Now make a small change to the dummy load and get a second set of readings, you can model (pretend) the amplifier output is a voltage source and an unknown impedance) at that particular power output, the operating point) and solve simultaneous equations to find it. The answer is only valid at that particular output power and load. You have performed a small signal linearisation about a particular operating point. I think this is called the load pull technique.
Isolation: I shall mainly ignore this, apart from one particular parameter. Some amplifiers have an annoying feature where if they are outputting to a device whose internal impedance varies then you experience variations in input impedance, an amplifier is said to be Termination Insensitive if it doesn't do this.
The particular amplifier I am testing here is known to be a TIA - a Termination Insensitive Amplifier I have simulated it in LTSpice, It is a bit fiddly to measure it in real life. You need to take a number of Zin and Zout measurements with differing load impedances. I will use 25, 50 and 100 Ohms and see what happens.
Noise figure/ Noise factor/ Noise temperature: These measure the same thing and are related to each other by simple formulae. I am still working out how to do this. The traditional method uses a noise source of known value (a "calibrated" noise source) and takes two readings, with it switched on and off. I do not yet have a source and they are expensive. The related topics of measuring Signal to noise ratio and sensitivity( Minimum Discernible Signal (MDS)) can wait until I have a complete receiver built.
Power Consumption/Efficiency: The output power and the power consumed by the Power supply contribute to the efficiency. Easier to do with simulation than actually measure. More important with the final power amplifier. To discuss this we should discuss amplifier Classes. Remembering that it is hard to generate an output voltage that is bigger than the power supply. (or twice the supply if you have collector/drain loads that are inductors)
A simple amplifier with a sine wave applied to it has an input that swings positive and negative (and usually passes through a capacitor). In a single-ended power supply, e.g +12V and Ground. The output can probably only swing plus or minus 6 volts. (actually 0 to +12V but if you use a capacitor you can consider it to be AC.) This means the amplifier output is sitting halfway between 0 and +12 when no signal is applied. This usually means there is base current bias applied and the transistor is half on. If it is half on, it is wasting power and the power consumption is maybe 50% of what you see with a big signal passing through.
However, at least the output is faithfully following the input even if several times bigger (the gain). This shows linearity. That's class A. I will discuss the other classes when testing high power amplifiers. Most transceivers use Class A for all but the final transmit amplifier to minimise distortion, we accept some distortion in the finals to keep the power consumption efficiency low where consumption is likely to be highest.
A recent topic is that power consumption efficiency matters in the first stage of a receiver. It affects battery life if you are portable. An easy but inefficient way to get good strong signal handling and coping with nearby strong signals whilst receiving weak signals is to pass a high standing current (known as the quiescent current) down through the active device, or to parallel the active devices - some high end receivers use four FETs in parallel - and hence consume four times the current, Might only involve less than 100mA but it will affect battery life. So a compromise must be reached and it is worth measuring the power consumption when testing an amplifier.
---
Here are some practical tests I undertook on the three transistor TIA amplifier used in the uBitx, the unit I tested had the 2n3904s swopped for BFW93s to improve noise figure. I also simulated the circuit in LTspice.
My first test was to measure OIP3, I used my homebrew Two Tone Oscillator with its output reduced by variable attenuator set to 30dB and fed the amplifier to the Spectrum Analyser - after checking it was below -10dBm where the SA has better linearity.
I got the waveform below;
So the Pout of the first tone, f1=13.035MHz is -12.9dBm and the IMD of twice f1 minus f2 is -67.7dBm (at 13.021MHz). The OIP3 is (Half the difference of the IMD and POUT) - POUT
i.e (67.7-12.9)/2 + (-12.9) = +14.5dBm,
not brilliant but ok. Perhaps the BFR93AW are poor performers, I will repeat the experiment with 2N3904s. I ran the BFR93AW version with 35, 25 and 40 db of attenuation and got OIP3 of +12.8dBm, +14.25dBm and +12.15dBm. The slightly worse figures at low signals might be evidence of some leakage direct to the SA so a figure of +14.5 dBm is probably the right one. (They should all be the same)
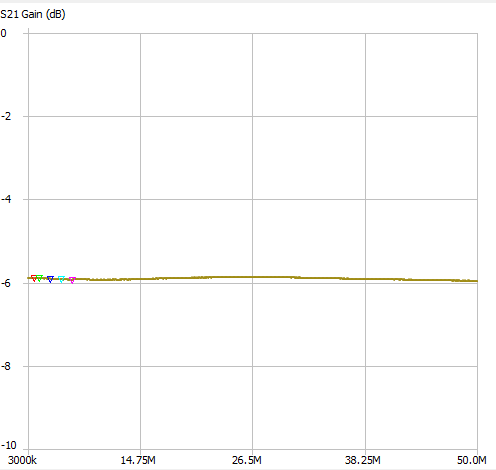
My next measurements used the NanoVNA, I used an inline 20dB attenuator, sometimes on the input, sometimes on the output of the amplifier.
S21 is the gain, but as I had a 20dB attenuator in circuit the gain is actually +14, nearly +15 dB and the frequency response is very good - In real life I will have filters either side of all the amps so the three dB points are irrelevant.(I think)